![]()
最適化
![]()
最適化とは、与えられた条件の中で、いろいろな選択肢の中から一番良いものを選ぶ問題の総称です。問題は数理的に与えて、数理的な方法で解きます。具体的には、n次元の実数ベクトル x (n個の数字の組:変数といいます)で、与えられた不等式・論理式など条件を全て満たすものの中で、ある、関数 f(x) (目的関数といいます)を最大にするようなものを求める、という問題です。世の中、数字で与えられるものばかりではない、とは思いますが、例えば、距離や、値段、時間などは数値で表せますし、ある事柄をやる/やらない、物を買う/買わないなどの選択も、0,1 の数字で表すことができます。
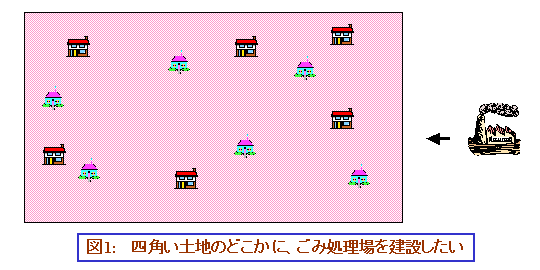
簡単な例を見てみましょう。今、あるとても広い長方形の土地のどこかに、ごみ処理場を作る計画があるとします。ただ、場所は決まっていません。土地の中には n 軒の家があります。どの家の人も、近くにごみ処理場があるといやなので、なるべく、どこの家からも離れた場所に作ることにしたいと思っています。どこの家からも離れた場所、というのでは今ひとつハッキリしないので、ここでは、各家からの距離の和が最大になるような場所にごみ処理場を建てる、とします。
まず、場所を x 座標と y 座標の値で表すことにします。家 i
の座標を (xi,yi) としましょう。
今、場所 (x,y) にごみ処理場を作るとすると、家 i
からごみ処理場までの距離は
{ (x-xi)2 + (y-yi)2 }1/2
になります。ですので、この総和が最小になるような場所を探せばいいわけです。ごみ処理場は、長方形の土地のどこかでなければならないので、x
と y
はそれぞれ、ある範囲の中に入っている、つまり、与えられた上限よりも小さく、与えられた下限よりも大きくなる必要があります。この例では、変数は
x と y、条件は、x と y の上下限 ( l<x<u
のような形で与えられます)、目的関数は各家からの距離の総和です。

この、最適化問題を解き、出てきた解が示す場所にゴミ処理場を建てれば、どの家からも遠いような場所にゴミ処理場を建てられるわけです。
この例ではゴミ処理場を考えましたが、スーパーの建設となると、なるべくどの家からも近い方がいいので、距離和を最小化する問題を考えればよいでしょう。消防署を作るのであれば、「どの家にも何分以内で行ける」ような場所に作るのがよいので、最も遠い家までの距離が短くなるようにすれいいわけです。他にも、同じ施設をいくつか作る問題、学校をいくつか作って、上手に区割りする問題など、いくらでも発展して、世の中のいろいろな場面で最適化が使えるのです。
最適化問題で、値を変化させるものを変数といいます。最小にしたい、あるいは最大にしたい値、あるいは関数値のことを目的関数といいます。変数が守るべき制約条件を制約といいます。この例では、x と y が変数、各家からの距離和が目的関数、x,y は四角の中に入る、が制約になります。目的関数と制約が全て線形である最適化問題は、線形計画問題と呼ばれます。この例では、目的関数が線形ではないので、線形計画にはなっていません。
線形計画問題は古くから研究されていて、シンプレックス法や内点法という、線形計画を短時間で解く方法が発見されました。ですので、その方法に基づいてプログラムを作ると、それなりに高速なソフトが作れます。近年、シンプレックス法のプログラムを高速化する研究も進み、10年前には5千変数の問題を解くのに1時間以上かかっていたのが、商用のソフトなら5万変数ぐらいの問題が、1時間かからずに解けるようになりました。現在、変数の数が10万くらいのものまでは、パソコンでもなんとか1時間程度で解けるようです。
上記の、処理場建設場所を選ぶ例は、凸2次計画と呼ばれる問題の1つです。凸2次計画は、制約及び目的関数が、凸2次関数か線形であるもののことです。この「制約が凸である」というのは、それぞれの2次の制約が、「放物線、あるいは楕円の内側である」という制約になっていることです。凸2次計画に関しても研究が進んでいて、線形計画ほどではないですが、短時間で解けるようになりました。変数が1000くらいの問題なら、パソコンでも1時間程度で解けます。

この図のように、最適化問題の中でも、いくつかのものは、商用のソフトを使って短時間で解けます。今、最適化したいなと思っている問題が、上記のごみ処理場の問題のように、凸2次計画なり線形計画になるなら、商用のソフトで簡単に最適な解が見つかるわけです。しかし、世の中の最適化問題は、どちらかというと、線形計画や凸2次計画にはならないものの方が多いのです。例えば、ごみ処理場の問題では、処理場を作ってよい土地が四角形でなく、変な形になったり、いくつかの分断された土地のどこか、というようになったりすると、凸2次計画ソフトでは解けなくなってしまいます。
このように、簡単には解けない最適化問題として、整数計画というものがあります。いくつかの変数に対して、「この変数は整数でなければいけない」という制約が付いたものです。物を買う個数、作る個数などが、最適化したい変数に入っている場合、「0.7個買う」とか「0.15台作る」とかいったものは実現できないので、自然な条件です。ですので、整数計画は速く解けるとうれしいのですが、残念ながら最適解を求めるには、変数が100程度でも、パソコン程度では1日では到底解けなくなります。スーパーコンピューターでも、かなり苦しいでしょう (一般的な話です。簡単に解ける種類の整数計画もあるのですが)。 たとえ今のコンピューターの速度が1万倍になっても、解ける問題の大きさは、10ぐらいしか増えません。コンピューターの高速化がいくら進んでも、こういう問題を解く、という観点からは、絶望的なわけです。
こういった難しい最適化問題をいかに速く解くか、という研究も行われています。まだまだ、大きな問題が解けるレベルにはなっていないのですが、それでも、何も考えずにプログラムを組むよりは、1万倍も、1億倍も高速に問題を解けるようになりました。
難しい最適化問題に対しては、近似解法という方法も研究されています。これは、「たとえ最適な解ではなくてもいいから、短時間で、目的関数が最適になるべく近い解を見つけよう」という方針で設計されたものです。短時間で、ある程度良い解が見つかるのが特徴なのですが、どれくらい最適解に近いか、つまり精度に関してはなんの保証も得られない、あるいは、おおざっぱな精度保証しか得られない、というのが普通です。この問題の最適解を知りたい、という目的には使えませんが、例えば、今のプランよりも良いプランがあったら、それに乗り換えたい、という目的の時には、問題なく使えます。こういった近似解法も、精度をなるべく良くして、大きな問題を解こうとなると、時間がかかります。ですので、アルゴリズムの研究が役に立つのです。
![]()