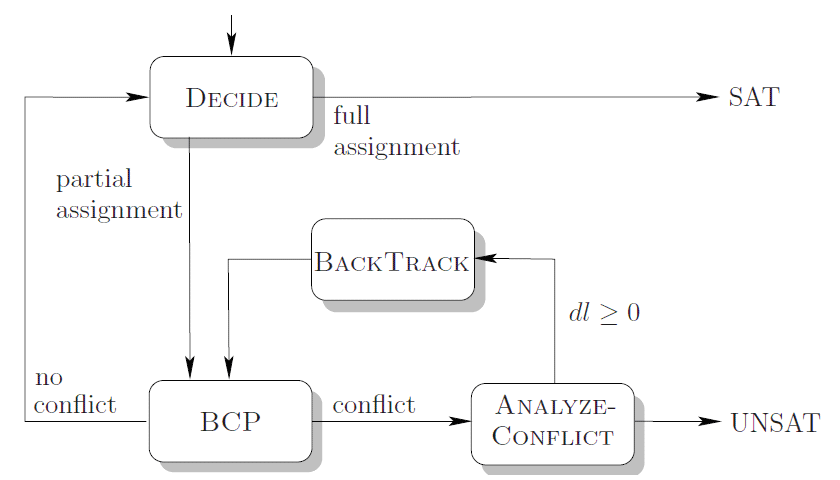
図1: miniSATスタイルのSATソルバ・アーキテクチャ
今年度は2つの実験を行った
SMT(Satisfiability Modulo Theory)は決定手続きが存在する1階の理論ソルバを命題論理SAT (Satisfiability)の枠組みに統合して構成された自動検証エンジンである。応用に合わせて理論ソルバを用意することで、SMTはハイブリッドシステムの自動検査を含む様々な場面で使われている。今後の自動検証ツールを考える上で必須の要素技術になっている。OpenSMTはオープンソースのSMT向けC++フレームワークであって、必要に応じて新たな理論ソルバを組込み拡張することができるという特徴を持つ。本実験ではOpenSMTを拡張するという観点から、その基本的なアーキテクチャの調査を行った。
SATは命題論理式の充足可能性判定問題の名称(Satisfiability)である。与えられた命題論理式を真とするような命題変数の真偽値割当てがあるかを判定する。たとえば、p、q、rをtrueあるいはfalse値をとる命題変数とする時、論理式 p ∧ (q ⇒ r) がtrue となるような値の組を求めれば良い。素朴には、式に現れる全ての命題変数にtrueあるいはfalseを設定して、式全体の真偽値を計算すればよい。これは自明な方法であるが計算の手間が大きい。実際、代表的なNP完全問題として計算量理論の教科書に必ず説明されている。SATソルバの技術は種々のヒューリスティックスを考案し、判定を高速化することある。標準的な方法は、1960年、1962年に発表されたBCP(ブール制約伝播)を利用したDPLL(Davis-Putman-Logemann-Loveland)アルゴリズムである。DPLLは対象の命題論理式をCNF(連言標準形)とする。これ以降、多くのSATソルバはCNF(clausal form)を対象としている。
1990年代に入って、SATソルバの高速化技術が進展し、Conflict-Driven Backtracking という方法を用いた探索の効率化手法が考案された。また、SATソルバの性能比較コンテストを実施する等の理由もあって、入力命題論理式の表現形式を標準化しファイル形式DIMACSが整備された。種々のヒューリスティックスを比較検討ならびに手軽に実験したいということから、オープンソースのソルバminiSATが開発公開されるに至った。無駄をそぎ落としたコードであり、性能面でも最先端のツールになっている。図1に、最近のminiSATスタイルSATソルバの制御アーキテクチャを図示した(文献2による)。
SATソルバは命題論理式を対象とする自動検証の技術である。種々の応用問題(スケジューリング問題、有界モデル検査、自動テスト生成、等)を命題にエンコードする方法がとられた。一方、整数の大小関係などを含む場合、真偽値判定を行うために、整数演算に関する処理が必要になる。変数x、yが整数値をとるとする時、整数演算を含む論理式 (2x - y < 2) ∧ (¬(x < 3) ∨ (x - 3y < 0)) の真偽判定を考える場合に相当する。整数に関する推論が必要となる。そこで、SATの枠組みに他理論ソルバを組み込むという発想が生まれた。理論ソルバをTとパラメータのように表現したアルゴリズムDPLL(T)が提案された。図1との比較でDPLL(T)を図2に示す(文献2より)。
図2からわかるように、BCP処理部から理論ソルバ(DeductionとAddClauses)を呼びだしている。
DPLL(T)の枠組みが有効であるためには、次の2つの観点を考える必要がある。
第1の点については、決定可能な1階論理の部分体系が理論的にわかっている。たとえば、文献1の表3.1には、特に、プログラムの性質を検査するために有用な体系(データ構造、配列、などを含む)が整理されている。第2の点については、Nelson-Oppenが組み合わせ可能な体系の条件を理論的に明らかにした。なお、文献3は本技術に関する網羅的なハンドブックである。蛇足であるが、数に対する四則演算を扱おうとすると、決定不能となる。万能ではないことを忘れてはならない。
以上に述べた技術の流れの中で、2009年University of Lugano(スイス)を中心にOpenSMTの開発が始められたと考えられる。SATソルバにDIMACS形式があるのと同様に、SMTソルバの入力形式SMT-LIBの標準化も同時進行である。SMTでは組み込む理論ソルバ個別の情報(台集合の宣言、演算子の構文、など)を明示する必要があることから、ファイル形式を超えた「言語」SMT-LIB v2として整備が進められている。SATと同様にSMTのコンテストも毎年、開催されている。
OpenSMTのアーキテクチャ上の特徴は、図2のBCP等の基本的な処理にminiSATを利用することである。図3で、T-Solverは理論ソルバを示す。
図3は概念 アーキテクチャであって、実際のC++フレームワークでは図4のような構成をとる。すなわち、EUF(Equality with Uninterpreted Functions)のソルバを特別扱いしている。ここで、EUFは、関数記号 f が具体的な関数本体の定義がなく、関数記号だけを用いて表した論理式 ¬(x = y)∧(f(x) = f(y))や(x = y)∧(¬(f(x) = f(y)))等を対象とする。前者は充足可能(たとえば、x=0、y=1、f(0)=0、f(1)=0、とすれば良い。)であるが、後者は充足不能になる。また、EUFは他の体系と組み合わせて使われることが多い。たとえば、論理式 (x > 3)∧(f(x + 2) = f(y))∧(¬(x = y))は、EUFと整数演算を組み合わせている。このように、多くの体系がEUFと組み合わせて表現した命題を扱うので、EUFを共通処理として実現することが好ましい。なお、図4で、各々、DL(Difference Logic、時間オートマトンのクロック制約で利用)、LRA(Linear Real Arithmetic)、BV(Bit Vector)である。
最後に、図5が、現時点(2010年秋)のOpenSMTクラス図(主要部のみ)である。
OpenSMTを拡張して新しい理論ソルバを組み込む際には、クラスOrdinaryTSolverのサブクラスとして実現する。
現在、実験を継続しており、「有界の集合と関係」を扱える理論ソルバの開発を行っているところである。本ソルバは文献4に述べた応用を想定している。CPSの問題を直接解決する検証エンジンではないが、OpenSMTの利用技術習得という点で有用と考えている。