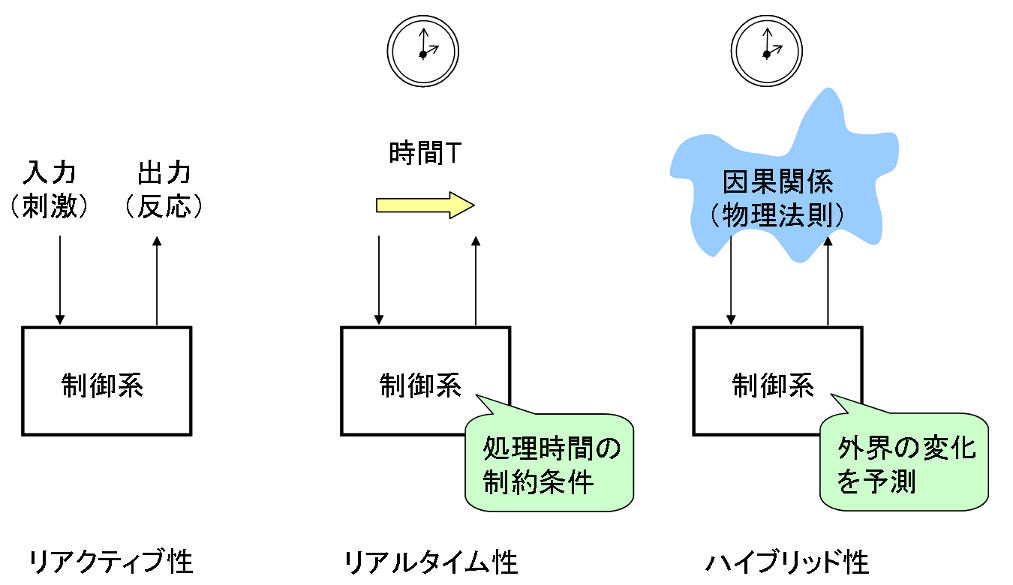
図1: 制御システムの分類
CPSの技術要素を、「離散と連続」という側面を中心とするハイブリッドシステムから考える。図1に制御システムの模式的な説明を図示した。
制御システムは入力(刺激)に対して出力(反応)を計算するリアクティブ性が基本となる。制御対象(外界)からセンサーを通して入力を得て、計算結果をアクチュエータに出力する。計算処理は瞬時に行われると仮定する。あるいは、外界が変化する周期に比べて圧倒的に制御システムの計算処理が速いと考えても良い。リアクティブシステムは離散的な状態変化に基づくとして状態遷移系として表現できる。たとえば、有限オートマトンやプロセス計算などの理論が知られている。
一般に制御対象は実世界で作動するのでニュートン時間で変化することから、入力から出力を計算する処理に時間的な制約条件がつく。想定の時間内に計算結果(出力)を得るリアルタイム性が求められる。この時、計算処理が決められた時間内に終了すれば良く、制御対象は入力と出力の時点で変化しないと仮定する。これを、同時性仮説(Synchrony Hypothesis)と呼ぶ。リアルタイムシステムは時間という連続量を取り扱う状態遷移系である。たとえば、時間オートマトンや時間付きプロセス計算などの理論が知られている。
実際は、制御対象あるいは外界は、因果的な法則にしたがって状態を変化させる。伝統的に、実世界(物理世界)の物体はニュートン方程式などの古典物理の法則に支配されると考える。入力時点から出力時点までに時間が経過することから、支配する物理法則にしたがって状態を変化させる。逆に、制御システムは、物理法則を用いた変化の予測を行うことで出力を計算する。通常、物理法則は微分方程式で定式化されているので、制御システムは連続量の計算が必須となる。リアクティブシステムでもあることから、有限オートマトンと微分方程式の統合の形をとる。離散と連続という2つの特性を持つことから、ハイブリッドシステムと呼ぶ。なお、時間進行を表すクロックは時間による微係数が1(定数)となるような微分方程式であらわすことができる。したがて、先の時間オートマトンはハイブリッドオートマトンの特殊例になっている。
図1の制御システム、いずれの場合であっても、制御システムと同時に、外界の制御対象の性質も重要である。特に、ハイブリッド性を考える場合、外界が物理法則で支配される実体であり、これをプラントと呼ぶ。図2に、制御系とプラントを明示した模式図を示す。
制御系とプラントはフィードバックループを持つとみなすことができる。したがって、組込みソフトウェアはCPSの基本的な性格を持つことがわかる。また、図1のハイブリッドシステムのように制御系が外界(プラント)の変化を予測する場合、制御系自身が連続量を取り扱うハイブリッドシステムになる。図3にそのような制御系の模式図を示した。
図3では破線で示した系のブロックがフィードバック制御を実現する。一方、「離散遷移」はフィードバック制御のモードを切り替える役割を果たす。状態遷移システムで表現することができる。
次に、図2の要素をネットワーク結合した分散システムとする場合を図4に示した。各々がハイブリッドシステムであるような構成要素がメッセージ通信するというアーキテクチャである。最近の車載システムが多数のECUから構成されるリアルタイム分散システムであるという特徴をとらえた考え方である。
最初に、図1のリアルタイム性について、ソフトウェア工学の観点からの要素技術について考える[1]。一般にソフトウェアシステムはマルチタスクであり、OSを用いるか否かによらず複数タスクにCPUを適切に割り当てる「スケジューリング」が大切である。特に、リアルタイム性が重要なシステムではタスクの時間特性を考慮する必要がある。リアルタイム・スケジューリング技術の研究開発が盛んに行われている。
リアルタイム・スケジューリングの問題は、多くの場合、周期タスクを対象として議論される。各タスクは、たとえば(T、D、r、C)というような時間特性で特徴つけられているとする。ここで、Tは周期、Dはデッドライン、Cはタスク実行時間、rはリリース時刻、と呼ぶ。特に、タスクはプリエンプティブとする。この時、スケジューリング問題は、デッドライン違反が起こらないように、タスクの実行順序列を決定することである。
スケジューリングでは、時間が2つの側面で考慮されていることに注意しなければならない。第1に、タスク実行時間Cである。最終的なプログラムとハードウェア(CPU、メモリ、等)の諸元が決まると、タスク実行に関わる時間を、たとえば、実測することができよう。この値をCとする。一方、ソフトウェア開発の立場からは、実測によらないでCの値を見積もりたい。特に、最悪実行時間WCET(Worst Case Execution Time)を知る必要がある。たとえば、基本的な文の実行を1単位に選び、プログラムを対象とした静的解析によって値を求める。プログラムの基本的な性質は機能振る舞いで特徴つけられるのに対して、実行時間という観点からの非標準解析の一種である。計算結果は、連続的な値として表現される。第2に、スケジューリングの結果は、時間軸に沿ったタスク切り替え事象列であるという点である。通常、タスク切り替えは任意の時刻で発生するわけではなく、切り替え周期が決まっている。この周期を単位とする離散的な時刻を取り扱えば良い。
スケジューリングの技術は、スケジューリングポリシー(同時に実行可能なタスクから選択するタスクを決定する時に用いる優先度を決める戦略)の性質、タスク間の実行順序の相関等の制約条件がある場合のスケジューリング、非周期タスクを考慮したスケジューリングなど、現実のシステムに近い状況を反映した方法の研究が進められている。
WCETはプログラムに対する最悪実行時間の見積もりである。一方、開発上流工程の設計物を対象として、時間的な特性と機能振る舞いを同時に取り扱いたいことが多い。そのための表現と解析の方法として、時間オートマトンが考案された。特別なクロック変数を持つオートマトンであり、たとえば、UPPAALが有名である。時間概念を持たないオートマトンを対象とするロジック・モデル検査と同様に、到達性(Reachability)の検査が可能である。また、時相的な性質としては限定されたCTL(計算木ロジック)を性質表現に用いることができる。時間オートマトンの組み合わせは同期積(Synchronous Product)の方法を用いる。遅延のある通信チャネル等をモデル化する時には、時間オートマトンを用いて明示的に表現しなければならない。
歴史的には、時間オートマトンの後、その一般化として、ハイブリッドオートマトンが考案された。繰り返しになるが、時間進行を表すクロック変数x(t)は時間による微係数が1(定数)となるような微分方程式であらわすことができる。すなわち、 dx/dt = 1 である。これを dx/dt = f(x) のように拡張すれば良い。一方、到達性が決定可能になるのは、関数fがxについて線形であるような場合、すなわち、線形ハイブリッドオートマトンだけであることが知られている。
一方、図2あるいは図3のようなハイブリッドシステムでは、プラントや制御系の制御ロジックを微分方程式で表現するのが都合が良い。実際、制御工学は、制御系とプラントを含む全系が安定であることを、微分方程式の解の性質に関する議論に帰着させて論じる。そこで、フィードバックループのある微分方程式系を簡便に書き表すことが要求される。
産業界では商用のツールMATLAB/Simulinkが使われている。図3のように離散制御系(状態遷移系)を必要とする場合、StateFlowを組み合わせて使う。StateFlowはUMLの状態遷移ダイアグラムのもとになったD.HarelのStatechartsに影響を受けている。なお、欧州では、MATLABに対抗する動きがあり、20-Sim、Scilab、MODELICA 等がある。モデル記述の実行シミュレーションを行うことで、設計結果を確認することができる。
自然な発想として、たとえば、Simulink(離散遷移を表現するStateFlowを含むとする)を、ハイブリッドオートマトンに変換して、自動検査することが可能であるかを試みたくなる。実際、そのような研究としてCheckMate があった。その他、HybridSALも似た狙いを持っていた。なお、HybridSALはバックエンドのエンジンとしてSMTソルバ Yicesを用いた。
現在も、いくつかの研究プロジェクトが進行中であるが、現時点では、次のように考えられている。一般に、あるモデル記述(この場合はSimulink)を数学的な形式(ハイブリッドオートマトン)に変換する場合、モデル記述の操作的な意味が曖昧さなく明確でなければならない。一方、そもそも、Simulinkは実行シミュレーションによってモデル記述の妥当性確認(validation)を行うツールであった。そのため、Simulink言語というものは明示的に存在せず、ツール環境が含むシミュレータが実行意味解釈を与えている。その結果、一意的に決まるような変換の方法を確立することができないという問題がある。
ハイブリッドシステムの形式検証に関わる研究では、入力のモデル記述言語も重要な検討対象とするのが普通である。汎用のモデル記述言語を考案することが可能か、難しい問題であろう。たとえば、KeYmaeraは、最近の研究として評価が高い。
ここで述べた技術は教科書[2]がカバーしている。表1に目次構成を載せた。残念ながら、ハイブリッドシステムの解析・検証については触れられていない。教科書は学部学生向けであり、ハイブリッドシステムの解析は、高度すぎるからであろう。
|
|
組込みソフトウェアの開発技術は、歴史的には、リアルタイム性やハイブリッド性を中心に発展してきた。今、CPSを新たな情報学の規範として考えて、科学的な見地からの研究を系統的に実施する機運が高まっている。そのキーワードは定量性(Quantitative)である。定量性に対する取組みには2つの観点がある。
前者は、ハイブリッドシステムや数値計算の高信頼化や自動解析に関する。数値計算プログラムでは計算誤差によって結果が異なるという問題がある(たとえばS.Rumpの問題)。精度保証付き数値計算の方法として、区間算術演算やアフィン算術演算の方法が知られている。
ハイブリッドシステムの性質解析を行う場合には、計算精度の問題が深刻になる。たとえば、計算誤差によって到達性解析の結果が異なる、などが起こり得る。そこで、Simulink等のモデル記述シミュレーションを行う際に、区間算術やアフィン算術の技術をベースとして、数値誤差の観点からの安定性(ロバストネスと呼ぶ)を解析する研究がある。
後者は、通常のプログラムやモデル記述を対象とした静的解析の技術によって、対象に内在する数値的な特性を抽出するものである。先に述べたWCETは、その古典的な問題のひとつである。性能や故障確率の解析も重要な応用である。最近の関心は、「どのくらいセキュアか」、「どのくらいエネルギーを使用するか」、「どのくらい2つのモデル記述が似ているか(定量的な双模倣関係)」などである。
この技術領域では、ERCIM (European Research Consortium of Informatics and Mathematics)のワーキンググループMLQA (Models and Logics for Quantitative Analysis)が2009年に設立され、学術的な研究活動の中心(QAPL Schoolを主催する等)になっている。
モデリングという言葉には少なくとも2つの意味がある。考察対象の抽象的な描画を作成することという一般的な意味と、UMLの用語としての狭い意味がある。UML(Unified Modeling Language)では、プログラミングに対比させてモデリングと呼ぶ。プログラミングが(実行可能な)プログラムを作成する活動であるのに対して、UMLモデル記述(ダイアグラム)を作成する活動をモデリングと呼ぶ。そもそもは、第一の一般的な意味でモデリングと呼んでいたが、その後の技術発展の中で、特別な意味を与えるに至った。一方、ソフトウェア技術を論じる際には、2つの意味が混在している。ここでは、一般的な意味での「モデリング」を考える。
利用者の振る舞いが重要なCPSがある。たとえば、車載システムを考えた場合、運転者は自身の感覚に基づいた判断からブレーキやアクセルを作動させる。その結果が、エンジンスロットル制御のソフトウェアに反映される。運転者の誤使用であっても車載システムの不具合と認識されることもある。一般にシステム利用者の振る舞いを開発時に予測することは難しい。しかし、開発の拠り所とした前提条件を明示しておくことは大切である。
モデリング結果は、何らかの記法あるいは言語で表現されたソフトウェア要求文書SRD(Software Requirements Documents)になる。たとえば、J.-R. Abrial氏は、要求項目を数学の定理のように簡潔に、かつ、後の参照が容易になるように表現することを推奨している[3]。記述内容に応じて、FUN(機能要求)、ENV(動作環境への要求)、SAF(安全性に関わる性質)、等に分類する。彼の手法は、要求項目を形式仕様言語Event-Bで表現し、リファインメント技法に基づいて仕様の詳細化、具体化を行う、というものである。リファインメントの各ステップを定理証明の方法を用いて形式検証するので、「構築からの正しさ(Correct by Construction)」を達成することが可能になる。
Event-Bでは、リファインメントの出発点となる初期仕様が正しいことが前提である。その正しさを納得することは容易ではないことから、通常、自明な記述から出発する。たとえば、分散システムを対象としている場合であっても、初期仕様は単純な集中系として表現する。分散システムに特有の問題を避けることができる。リファインメントの後段で具体化すれば良い。
リファインメントと同様に大切な技法として、「仕様の分割(Decomposition)」がある。上にあげた分散システムの場合、送り側と受け側ならびに通信基盤に細分化した後は、両者を独立に考えるべきであろう。古典的な分割統治(Divide-and-conquer)の方法であって、何も特別なことではない。しかし、信頼性に重きをおく形式検証という観点からは、分割の技法は本質的な役割を果たす。これを説明するのに、分割と対比される方法「組み合わせ(Composition)」を考える。
組み合わせの考え方は、オブジェクト指向ソフトウェア技術の発展の中で、主として生産性向上の方法として発展してきた。品質を保証されたソフトウェア部品(コンポーネント)を組み合わせて目的システムを構築する。再利用性の高いコンポーネントが鍵となる。
信頼性の問題を考える際に、システムに期待する満たすべき性質を考える必要がある。一般的に、満たすべき性質を、安全性(Safety)と活性(Liveness)に分ける。安全性は「悪いことが起こらない」ことであり、システムが取り得る全ての状態を調べて、いずれも期待に反する状況にならないことを確認する。活性は「良いことが起こる」ことであり、システムの状態変化を追跡して調べる必要がある。特に、組込みシステムのように継続して作動するシステムでは、「どの時点からみても、その後に、良いこと(イベント)が起こる」ことになる。このような性質は、システムの状態列がループ状になっていて、さらに、ループ中で当該イベントが発生する場合に成り立つ。
今、2つのコンポーネントがあって、各々が活性を満たすとする。この時、各コンポーネントに着目した状態列はループ状になっている。ここで2つのコンポーネントを組み合わせることを考える。問題は、2つのループが1つの大きなループになり得るか、である。単純な組み合わせでは、全系が取り得る状態列は独立な2つのループを持つだけであり、その結果、各コンポーネントが持っていた活性を満たさなくなることがわかる。
このように、組み合わせの方法(Composition)は再利用に基づく生産性の向上には貢献するが、活性が重要になる組込みシステムの信頼性確保技術には不向きである。したがって、リファインメントと分割に基づく開発法が注目されている。なお、組み合わせ方式についても、信頼性確保の観点からの研究が進められている。いずれのアプローチが優れているか、多分に、思想的な面が大きい。まだ結論が出ていないというべきであろう。今後の研究進展が期待できる。