![]()
アルゴリズムとはなんでしょうか
![]()
※ 2012年12月24日、テレビ東京系列で放送される「青春アルゴリズム」で、このページの内容が引用されることになりました!
「アルゴリズム」というのは、コンピューターで計算を行うときの「計算方法」のことなんですが、広く考えれば、何か物事を行うときの「やり方」のことだと言っていいでしょう。その「やり方」を工夫して、より良いやり方を見つけよう、というのが、アルゴリズムの研究です。同じ計算を行うんだったら、いい方法でやればより速く計算できますね、ということです。
計算方法を工夫すると楽ができる、という例として、かの昔の高名な数学者(ガロアだったか、ガウスだったと思うんですが、なにせ、小学校のときに見た本の記憶なもので)の、小学校時代の逸話を紹介しましょう。彼が小学生だったとき、ある算数の授業で、彼の先生は、ちょっと楽をしようと思い、生徒たちにこんな課題を出したそうです。
「1から100までの数を全て足した数を計算しなさい」
これを計算するには99回足し算をする必要がありますから、しばらくは休めるなと思ったわけです。しかし、先生がやれやれ、と自分の席につこうとすると、生徒の一人だった彼は、たちどころに、「できました」と答えたそうです。そんなばかな、と先生がチェックしに行くと、確かに5050という正解が書いてあります。別に彼はそろばんの段位を持っていたわけではなく、計算が超人的に速かったわけではないのに、どうしてこんなことができたのでしょうか? その秘密は、彼の計算方法にあります。彼はこう考えました。
「1 と 100 を足すと 101、2 と 99を足すと 101、3 と 98 を足すと 101。このように、数を2つずつの組にすると、それぞれの合計が 101 になるように組み分けできる。組の数は全部で50。101 が 50 個あるのだから、全部あわせれば 5050だ。」
確かにこの通り。こういう風に考えれば、わざわざ 99 回の足し算をしなくても、全ての数の合計が求まります。このガウスの方法を一般的にすると、1 から n (nは偶数とします) までの合計を計算するには、(n+1) と n/2 をかければいいことになります。高校生の数学で出てくる、「等差数列の和」と同じですね。さて、この方法のすごいところは、n-1 回の足し算をしなければ求まらなかった答えを、足し算1回、掛け算1回、割り算1回でできるようにしたことです。1から100くらいだったら、ひょっとしたら、そろばん8段の人が99回足し算をするほうが、彼よりも速いかもしれません。でも、n が大きくなって、1万や1億になったら、いくらそろばんの人が速くても、彼にはかなわないでしょう。計算方法を工夫するだけで、莫大な手間を省略できる可能性があるわけです。
こういった計算方法の工夫は、何も数学的な計算だけでなく、データベースの検索などの作業にもあります。その例として、辞書の単語の検索の例を見てみましょう。コンピューターのディスクに辞書のデータがあって、この中から、指定した単語を探し出す、よくある検索の問題を考えましょう。さて、では、辞書から「アルゴリズム」という単語を見つけましょう、という検索問題を考えます。どうやって見つければいいでしょう? まず思いつく簡単な方法は、
・辞書を頭から調べて、一つ一つの項目と「アルゴリズム」を比較する。一致したら「見つけた」
という方法。広辞苑第5版の項目数は約23万だそうです。「アルゴリズム」はあ行で、前の方に載ってますから、この方法でやってもたぶん5000回くらいの項目と比較すれば見つかるでしょう。ですが、もっと後ろに載っている言葉ならば、もっと時間がかかります。広辞苑第5版の最後の言葉は「んとす」(終りな−、という意味だそうです)ですので、この言葉を検索するときには23万回比較することになるわけです。最近のパソコンは、だいたい1秒間に1000万回くらい計算ができます(だいぶいいかげんな表現ですが)。ですので、この23万回というのはそんなに莫大な数ではありません。普通にプログラムを組めば、1/50秒くらいで計算が終わるでしょう。この方法なら、プログラムを組むのも簡単だし、めでたしめでたしですね、といいたいところです。ですが、さて、皆さんが辞書を引くときに、こんな方法を使うでしょうか? 普通、辞書というものはあいうえお順でソートされているので、たぶん、こんな方法を使っていると思います。
(1) だいたい真中をえいや、と開く
(2) 調べたい単語がそこより前あれば、そこより前の部分の、後ろにあれば後ろの部分のだいたい半分を、またえいや、と開く
(3) 調べたい単語が見つかるまで、(2) を繰り返して、範囲を小さくして行く。
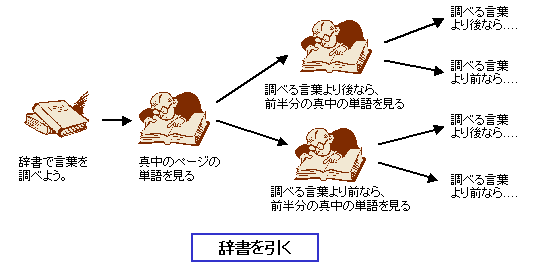
実際は、辞書には「あかさたな列」の見出しがついているので、最初の1文字で大体のあたりをつけて、その周辺を探すという方法をとっていると人が多いと思いますが、あたりをつけ終わった後、いよいよ探す範囲が狭くなると、こんな方法を使っていると思います。こういう方法を使えば、全部の単語を調べる必要なんてないんですよね。(この方法は、学術的には「2分探索」と呼ばれています)
コンピューターでも、プログラムの設計を変えれば、こういう方法で単語を検索できます。一回、真中を開くと、調べる範囲が半分に減るので、真中を開く回数は、単語数を n とすると、log2 n 回になります( log を知らない人は、気にしないで先を読んでください)。広辞苑の23万単語の場合は、18回、真中をえいや、と開けば、調べたい単語が出てきます。このスピードの違いはすごいですね。かたや 23万回の計算、それに比べて、かたや 18 回。1万倍くらい違います。
この例だと、どちらも1秒未満で計算が終わるので、見た目にはどっちも同じように見えます。ですが、もっと時間のかかる計算だったらどうでしょう。例えば、工夫すれば1秒ですむ計算が、工夫しないと1万秒かかるわけです。1万秒というと、およそ3時間です。工夫すれば1分の計算は、1万分かかることになるわけです。1万分はおよそ1週間。アルゴリズム、つまり計算のやり方をちゃんと考えてプログラムを組まないと、1分ですむはずの計算を、1週間かけて行うことになります。実際、インターネットのホームページ検索などは、10億や100億といった量のページ (広辞苑の1万倍くらいですね) に対して検索を行うので、検索方法の工夫をしないと、大変なことになるのです。
コンピューターの基本的な操作の1つにソートというものがあります。これは、めちゃくちゃな順番に並んでいるデータを、小さい順なり大きい順に並び替える、という操作です。この、ソートに対して、クイックソートという、良いアルゴリズムがあります。データが増えたとき、ソートにかかる時間がどれくらいになるか、下の図に比較表を作りました。

このように、良いアルゴリズムを使わないと、計算するのに大変な時間がかかることになるかもしれないのです。
逆に考えると、今一週間かかる計算が、ひょっとしたらアルゴリズムを工夫したら、1分で解けるようになるかもしれない、ということでもあります。最近のスーパーコンピューターを1億円くらいで買っても、パソコンの1000倍くらいしか速くなりませんから、なにかしらの計算の工夫でスーパーコンピューターを買うのと同じ効果が得られるかもしれないのです。全ての計算が速くなるわけではないですが、どの計算がどれくらい速くできるかを、アルゴリズムの研究をすることで解明できるわけです。
このように、いろいろな計算が(プログラムの書き方を変えただけで)どこまで高速に計算できるのか、また、高速に計算できる場合は、どんな性質を満たすのか、同じような計算でも、計算速度が大幅に異なってしまうのはなぜなのか、理論的に算定した計算時間と、実際に実験してみた計算時間がどの程度違うのか、そんなことを研究するのが、アルゴリズムの研究なのです。
![]()