![]()
近似解法
![]()
近似解法とは、主に組合せ最適化などの最適化問題を解く方法の1つです。
組合せ最適化は、線形計画のように、高速に最適解が求まることはまずありません。問題の大きさ(変数)が2,30程度でも、1時間くらいかかったりします。そこで、限られた時間、5分〜10分程度で、誤差が5%くらいであろうと思われるような解を求める、という作戦に基づいた方法が、ずいぶん研究されてきています。これが近似解法です。いろいろな組合せ最適化問題に対して、数多くの方法が発明されていて、それぞれ、長所短所があります。ですが、どの方法にも共通して言えることは、とても運が悪ければ、悪い答えが出るかもしれないけれど、たくさんの問題例に対して実験してみた結果、そんなに悪いものは出ない、ということです。近似解法を用いれば、問題の大きさが3000くらいまで増えても何とかなります。
近似解法は、大きく2つに分類できます。一つ目は、解の精度を保証することを目標にしているもの、もう1つは解の精度は保証はなくとも、なるべく良い解を求めよう、というものです。
前者の、解の精度を保証する、というものは、プログラムの見つける解の評価値(目的関数値といいます) が、最適な解の目的関数値に比べて、ある一定割合以上悪くならない、という保証があるような解法のことです。例えば、あるソフトがあって、このソフトが出す解のコストは、最適なコストの2割増し以上になることはない、という保証が付いている、というような感じです。
数学的にきっちりと保証をするのは、それほど簡単ではありません。そこで、あの手この手、様々なアイディアに基づいた方法が考えられてきています。例えば、制約条件を満たさないが、解の精度は十分であるような解を作り、その解を少しずつ変えていって、制約条件を満たすようにするものや、最適化問題の条件を緩めて線形計画問題にしてしまい、その最適解を使って、うまくもとの問題の解を作るもの、などです。この種の近似解法の研究をすると、興味深い数学的な性質がいくつも出てくるので、研究上、なかなかの人気者です。
さて、この「解の精度の保証」ですが、実用上はというと、良い精度保証はなかなかできません。解の精度が2倍 (コスト最小化をするのなら、最適なコストの2倍以下の解が得られる) や3倍、悪いものだと 10倍や20倍になるようなものが多いのです。後者の、精度保証のないほうの解法では、10% くらいの誤差のものが得られることが多く、この点は大きな課題です。また、計算に時間がかかる方法が多い、というのも課題です。今後、より精度を高めるにはどうすればいいか、計算の高速化をするにはどうすればいいか、などが研究されていくでしょう。
後者の、精度は保証はなくとも、なるべく良い解を求めよう、という方は、数多くの例題を解いても、精度の悪い解が出ないような、そんな方法を使おう、というものです。ひょっとすると、苦手な問題のタイプがあって、それらを解くとすごく精度の悪い解が出てくるかも知れないけれど、数多くの例題で実験してみたら、そんなに悪い解は出てこなかったから、だいたいの場合は大丈夫だろう、という論法です。これらの方法は、ヒューリスティックと呼ばれています。近年、その中でもメタ・ヒューリスティックと呼ばれるものが良く研究されていて、いい解法がいくつも発見されています。巷でよく見かける遺伝アルゴリズム、というのも、このメタ・ヒューリスティックの1つです。
メタ・ヒューリスティックの一番基本的なものは、近傍探索という方法です。これは、最初に1つ解を見つけて、解の評価値(目的関数値、つまり最適化したい値)が良くなるように、解をちょっとずつ変更していき、ちょっとの変更では値が良くならなくなったら、そこで終了、その解を出力しましょう、という簡単なものです。
例を見てみましょう。ある組合せ最適化問題の解を S とします。今、「ちょっとずつ変更する」こととして、S に要素 e を加える、あるいは S から e を取り去る、という変更を考えましょう。e をいろいろと変えれば、この変更方法を用いて、いろいろな解が得られます。得られた解の中に、制約条件を守っていて、目的関数の値が S よりも良いものがあったら、S を、その解に変更します。S よりも良いものがなかったら、そこで終了します。目的関数の値が良くなる間、次々に S を変更していくのです。
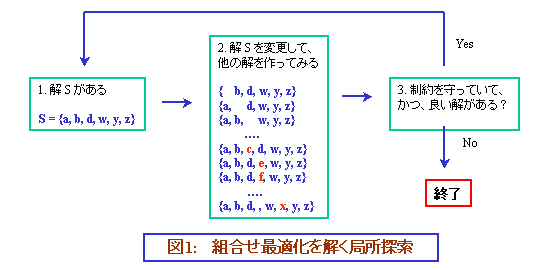
この「局所探索」という方法では、もっとも良い解、つまり最適解が得られるわけではない、というのは、直感的にすぐに分かると思います。1個加えたり減らしたりしたものの中に、今より良い解がないからといって、全体の中に今の解よりも良いものがない、というのは、性急な結論ですから。しかも、1個しか変更しない解しか見ていませんから、解の精度もそれほどよくありません。では、より精度を良くしたければどうすればいいでしょうか。ここで、工夫をするのがメタ・ヒューリスティックです。
工夫のやり方、その1つは、「1個加える/減らす」という変更を、「1個か2個加える/1個か2個減らす/1個減らして1個増やす」のように、変更の作業を大掛かりにしていくものです。この方法も、局所探索と呼ばれています。変更の操作で入れ替える個数を3個、4個と増やせば、それだけ計算に時間がかかるようになりますが、解の精度の向上は見込めるでしょう。
2つ目は、この局所探索を何回も行う、というもの。最初に与える解、つまり、局所探索を始めるスタート地点を変えれば、得られる解も変わるので、何回もやれば、そのうちにいいのが見つかるだろう、という発想です。多スタート局所探索と呼ばれています。簡単なアイディアですが、なかなか強力であることが報告されています。
もう1つは、「変更して得られたものの中に、S よりも良いものがない」ときに、そこで終了せずに、解が悪くなってもかまわないから、悪いなりにいいほうに移動してしまおう、というものです。ただし、次に、今いるところに戻ってきてしまうと、同じところを行ったり来たりしてしまうので、悪いところに移動するときは、「こっちに戻ってはダメ」という印を付けておきます。この方法はタブー探索と呼ばれています。
この他、解がよくなるほうに移動するばかりでなく、たまには(ある一定の確率以下で) 悪いほうにも移動するようにしよう、としている、アニ−リング法もあります。
遺伝アルゴリズムは、これらの方法とはちょっと発想が違っています。制約条件を守っている解を最初にいくつか作ります。それらの解から2つずつのカップルを作り(カップルを作る以外のやり方もありますが)、それぞれのカップルに対して、そのカップルの子供をいくつか作ります。子供は、そのカップルの解を切り貼りして合成して作ります。親の特徴を備えた子供ができるわけです。で、親と子供合わせた中で、良いものから順にある程度だけ残し、残りは捨てます。この作業を何回も繰り返せば、良い解の持つ特徴を備えた解がたくさん出てくるだろう、良い解の特徴を備えた解の中には、より良い解があるだろう、という発想です。
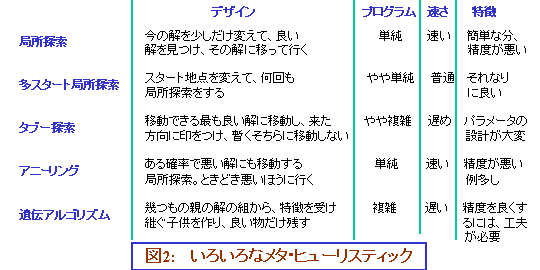
同じ組合せ最適化問題でも、近似解法によって、得られる解の精度は異なります。ある問題に対しては、アニーリングが精度の高い解を見つけても、他の問題では、アニーリングはぜんぜんダメで、遺伝アルゴリズムが良かったりと、問題によって、解法の性能も異なります。個別の解法でも、ちょっと設計を変えるだけで、解の精度が大幅に変化したりします。ですので、どの問題には、どのような方法をどのように使うと効果的か、それを調べる研究がたくさん行われています。
局所探索、アニーリングは比較的高速ですが、遺伝アルゴリズムとタブーサーチは時間がかかりことが多いです。ただ、時間をかけた分だけ出てくる解も良いものが多い、ということもあるようです。これらの近似解法に対しても、アルゴリズムやデータ構造の工夫による高速化は有効です。同じ原理に基づいて作られたプログラムでも、アルゴリズムの工夫、つまりプログラム設計の工夫によって速度が向上するからです。近似解法は莫大な数の方法が発見されてきているので、アルゴリズム的な研究は、これからどんどん、やることがあるわけです。
組合せ最適化は、線形計画や2次計画と異なり、精度の良い商用のソフトはあまり出ていません。組合せ最適化問題は、それぞれ独特の癖があって、なかなか、どの問題も精度良く高速に解けるソフト、というものは作れないのです。組合せ最適化は、非線形計画の1種ですので、非線形計画を解くソフトを使う、という手もありますが、ちょっと問題が大きくなると、とたんに良い解が出なくなり、企業活動で出てくるような、大きな問題は解けなくなります。組合せ最適化には、それぞれの問題にあった近似解法を使うことが重要なのです。さらに、近似解法自体も、アルゴリズムを工夫して、高速化しなければ、実用上はなかなか使えるものにはなりません。
大規模な組合せ最適化問題の場合、人間が解くと、1日2日かけて一生懸命解いても、あまり良い解が得られない、ということが多いものです。それに比べて、近似解法を用いた場合は、1時間程度で、だいたい、人間が解くよりも良い解を得ることができます。その結果、例えばコストが1割削減できるプランが見つかった、となれば、年間コストが1億なら、1000万円のコスト削減を行えるわけです。こういった意味でも、大規模な組合せ最適化を解く高性能な近似解法の開発は重要なのです。
![]()