![]()
スケジューリング問題
![]()
スケジューリングとは、いくつかの、やらなければならない仕事があるときに、どういう順番で仕事を進めればもっとも速いか、あるいは都合が良いか、その、最適な仕事をやる順番を求める問題のことをいいます。
簡単な例を下の図に書いてみました。ある夫婦がいて、ホームパーティーのために、お料理を作ろうと思ってます。作る料理は決まっていて、どうやって料理すればいいかもわかります。どの調理にどれくらい時間がかかるかも、かっこの中に書いてあります。料理が出来上がったらパーティーが始められるので(ただし、魚料理とお茶は遅れてもいい)、なるべく早く作り上げたいのですが、適当な順番で調理を進めると、やれコンロが足りないとか、スープ以外はできたけど、スープができるまでに30分かかるよ、とか、トラブルが発生します。さて、全部の料理がなるべく早く出来上がるために、最適な調理の順番を求めましょう、というのが問題です。

この例の場合は、こんな順番でやると早くできます。食事開始まで1時間、食事開始後10分で魚料理ができてお茶が入ります。
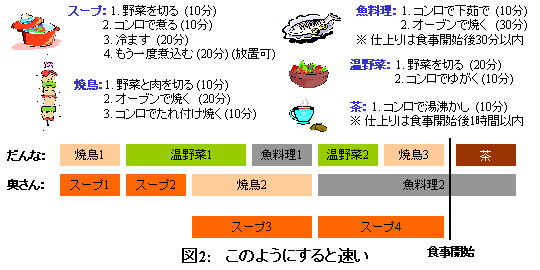
この例の場合は、2人ともきっちりと仕事ができますが、例えばコンロが1つしかないと、このように、最適な順番でも調理をみっちりできるわけではなくなります。適当な順番で調理をしたら、もっと作業効率が悪くなるでしょう。パーティーだったら、ヒマな人はお客の相手をしていればいいのですが、工場の作業のような場合は、なるべくヒマな人は少ないほうが良いですね。

このように、いくつかの作業を要する仕事がいくつかあって、納期、あるいは仕事の開始時期を守った上で、どれくらい効率良く (残業が少ないとか) するか、使う機械を少なくするか、等を最適化する問題が、スケジューリング問題です。似たような問題で、授業の時間割を決める問題とか、従業員の勤務表を作る問題もあります。
それぞれの作業が使う、機械、人などを資源と呼びます。同時に使える資源(機械の台数)に限りがあるので、ある機械を使う作業を同時にたくさん行うようにしてはいけない、という、制約条件を守る必要があります。この他、スープの例のように、ある作業が終わってから次の作業に入るまでに時間を空けなければいけない、あるいは逆に、ある時間以内に次の作業を開始しなければならない、という制約が付く場面もあります。いくつかの部品を組み立て、それらを組合せて製品を作るときのような場合は、部品の組み立てが終わってから、製品の組み立てを開始しなければならない、という制約もつきます。
これらの制約を守ったスケジュール、あるいは作業工程の中で、作業効率が最も良いもの、あるいは、忙しいときは納期遅れが最も少ないようなものを求める問題がスケジューリング問題です。製造工場の最適作業工程の自動作成、航空会社・鉄道会社などの運転手・搭乗員の最適勤務表作成、時間割作成などに使われ、応用範囲はとても広くなっています。実際に必要とされるスケジューリング問題では、守るべき条件にはどのような形のものがあるか、どういう条件がある問題が、どれくらいの速度で解けるのか・どういう方法だと速く解けるのか、なるべく速く、かつ、実際に使い物になるようなスケジュールを出すには、どういう条件を考えてどのような解法を使えばいいのか、などの研究を行うのが、スケジューリングの研究なのです。
スケジューリング問題は、配送計画などと同じく、大きな問題を最適に解くこと、つまり、必ず最適な解を見つけるようなプログラムを作ると、ものすごく長い計算時間を必要とします。例えば作業数20の仕事が20個ぐらいあるような、簡単な場合でも、おおよそですが、パソコンを使って解いても、1日くらいはかかります。問題によって、それこそ1分程度で解けるものもありますが、運が悪ければ、1日2日では済まなくなります。
実際に、工場などで解きたい問題は、それこそ、作業数が1000以上になります。このような問題に対して、真の最適解を求めるのは、ほぼ不可能です。そこで、近似解法といって、限られた時間、5分〜10分程度で、誤差が5%くらいであろうと思われるような解を求める、という作戦に基づいた方法が、ずいぶん研究されてきています。数多くの方法が発明されていて、それぞれ、長所短所があります。ですが、どの方法にも共通して言えることは、とても運が悪ければ、悪い答えが出るかもしれないけれど、たくさんの問題例に対して実験してみた結果、そんなに悪いものは出ない、ということです。このような方法を用いれば、作業総数が3000くらいまで増えても何とかなります。人間が解く場合、大きな問題になると、何人かが協力して作っても、誤差が20%の答えを得るだけで1日作業となることが多く、作業の効率化には大きな助けとなるようです。
現在、スケジューリング問題を解くソフトウェアがいくつか販売されています。これらのソフトは、主にディスパッチングという手法に改良を加えて作られています。このディスパッチングという方法は、それぞれの仕事に優先度を付けて、優先度の高い順に作業時間や資源(機械など)を割り当てていく、というものです。しかし、学術的には、この方法ではあまり良い解が得られない(場合によって異なりますが、近時解法に比べると、1-2割という感じでしょう)、ということもわかっています。速度はまあまあ速いのですが、作業総数が1万を超えたあたりで、計算時間が1時間くらいかかるようになります。ただ、プログラムの構造は簡単なので、製作者側から歓迎されているのと、優先度が高い仕事が必ず優先されることが保証されるので、その点が歓迎されています。
対して、近似解法でも、優先度の高い仕事をかならず優先するようにできます。しかし、普通は、一つの仕事の納期を遅らせて10の仕事の納期を守ることができたら、たとえ優先度が多少高くても、その1つの仕事の納期を遅らせるものでしょう。こういうふうに、多くの仕事がなるべく納期を守るようにしたい、という目的で問題を解くには、近似解法の方が優れているのです。
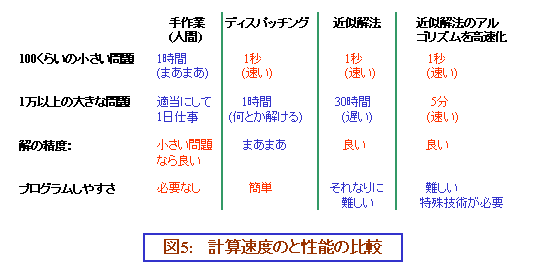
近似解法のプログラムを簡単に、工夫なしで組むと、かなり計算時間がかかるものが出来上がります。作業総数が1000くらいのものでしたら、計算時間はおよそ1時間程度になるでしょう。近年の、大型スケジューリング問題は作業総数が1万から10万くらいあります。このような大規模な問題を解こうとすると、簡単なプログラムでは1週間以上の時間がかかってしまいます。
普通は、たとえ小規模な問題でも、このような、計画、あるいはプランを決める問題では、問題を解きたい人が欲しいと思っているような答えをコンピューターがそのまま出してくれることはありません。条件や目的を数値化しているので、どうしても、人間の考えている条件と、コンピューターが理解した条件との間にギャップができてしまうからです。そこで、通常は、コンピューターの出した答えを人間がチェックして、「この部分は良いがこの部分はよろしくない」という点を探し出し、そういった解を出さないよう、条件を新たに付加してコンピューターに問題を解かせなおす、といった方法が行われます。こうして、コンピューターと対話して、人間の、あいまいな条件をコンピューターに理解させていくのです。そのためには、一回の問題を解く時間が、1分程度になる必要があります。一回解くのに10分も20分もかかるようでは、対話している人間がいらいらしてしまいます。
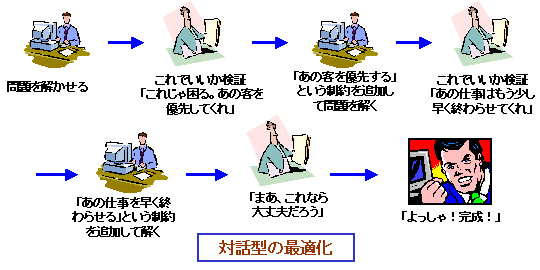
こういった対話型の最適化を行うためには、計算の高速化がかかせません。計算の高速化には、アルゴリズムの改良やデータ構造の工夫が不可欠です。今後研究を進めれば、各種のスケジューリング問題がそれこそ瞬く間に解けるようなものが、開発されていくでしょう。
現在でも、マイクロソフト・エクセルなどの表計算ソフトにも、スケジューリングを解く簡単なプログラムが組み込まれています。個人のスケジュールの管理などの小さな問題は、人が解いたほうが都合が良いですが、学校・学習塾などの時間割、小企業・病院などの勤務表作成などの問題は、人間がいいスケジュールを作ろうとすると、かなりてこずります(1日から2日かかるとようです)。現在のソフトでは、まだまだ、これら勤務表などの問題を精度良く解くには時間がかかります。今後の研究によって、個人ベースのスケジューリング問題を簡単に解けるようになるかもしれません。そうなれば、これらのソフトを使って勤務表作成問題を解く、ということがあたりまえになる日が来るかもしれません。
![]()