![]()
アルゴリズムってなんでしょか
![]()
※ 2012年12月24日、テレビ東京系列で放送される「青春アルゴリズム」で、このページの内容が引用されることになりました!
私の研究は、「アルゴリズム」と「組合せ最適化」です。ここでは、そのうちのアルゴリズムについて解説しましょう。
「アルゴリズム」というのは、コンピューターで計算を行うときの「計算方法」のことなんですが、広く考えれば、何か物事を行うときの「やり方」のことだと言っていいでしょう。その「やり方」を工夫して、より良いやり方を見つけよう、というのが、アルゴリズムの研究です。同じ計算を行うんだったら、いい方法でやればより速く計算できますね、ということです。
例えば、簡単な例。にんじんが星型の輪切りになっているもの、あれを、にんじん一本から30個作る方法を考えましょう。1例目として、まず、
・ 輪切りをたくさん作ってから、それぞれの角を落として星型にする方法
というのが考えられます。これだと、包丁を入れる回数は、輪切りを作るのに31回(端っこを落とすのに2回使ってます)、それぞれを星型にするのに、10回、包丁を入れるので、合計 31+10*30 = 331 回、包丁を入れます。結構大変ですね。でも、ちょっと工夫をすると、
・まず、にんじん本体を星型に切って(断面が星型の棒になります)それから輪切りにする
という方法を考えると、
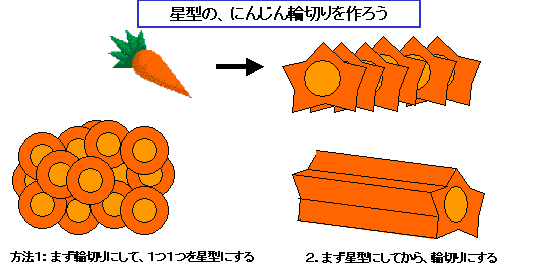
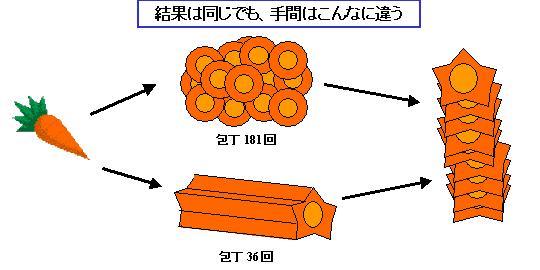
これは、本体を星型にするのに10回、輪切りにするのに31回なので、なんと包丁を入れる回数は 41 回に減ります。にんじん本体を星型に切るのは、輪切りにするほど速くはできないとは思いますが、3倍ぐらいのスピードにはなるでしょう。まあ、あたりまえのアイディアなんですけど、これはすごいですね。331回から 41回ですから。同じ星型の輪切りを作るのに、ちょっとやり方を変えただけでこの違い。やり方かえるだけで作業効率が3倍違うんですから、がんばって修行して包丁さばきのスピードをあげる前に、「やり方」の工夫を考えたほうがよさそうです。
キャベツの千切りなんかでも、葉っぱを一枚一枚千切りにするより、10枚くらい重ねてやったほうが、10倍スピードが速くなりますよね。こういった工夫がなかったら、とんかつ屋さんで山盛りキャベツを食べる、なんて楽しみは味わえなかったでしょう。
この「やり方の工夫」というのは、包丁さばきだけに限ったことではありません。コンピューターの計算方法にもあります。簡単な例は、辞書の単語の検索です。コンピューターのディスクに辞書のデータがあって、この中から、指定した単語を探し出す、よくある検索の問題ですね。さて、じゃあ、辞書から「アルゴリズム」という単語を見つけましょう、という問題を考えます。どうやってみつければいいでしょう? まず思いつく簡単な方法は、
・辞書を頭から調べて、一つ一つの単語と「アルゴリズム」を比較する。一致したら「見つけた」
という方法。広辞苑第5版の項目数は約23万だそうですが、「アルゴリズム」はあ行ですから、この方法でやってもたぶん5000回くらいの項目と比較すれば見つかりそうですね。ですが、もっと後ろに載っている言葉ならば、もっと時間がかかるでしょう。ちなみに広辞苑第5版の最後の言葉は「んとす」(終りな−、という意味だそうです)ですので、この言葉を捜すときには約23万回比較するわけです。最近のパソコンは、だいたい1秒間に1000万回くらい計算ができます(だいぶいいかげんな表現ですが)。ですので、この23万回というのはそんなに莫大な数ではありません。普通にプログラムを組めば、1/50秒くらいで計算が終わるでしょう。この方法なら、プログラムを組むのも簡単だし、めでたしめでたしですね、といいたいところですが、さて、皆さんが辞書を引くときに、こんな方法を使うでしょうか? 普通、辞書というものはあいうえお順でソートされているので、たぶん、こんな方法を使っていると思います。
(1) だいたい真中をえいや、と開く
(2) 調べたい単語がそこより前あれば、そこより前の部分の、後ろにあれば後ろの部分のだいたい半分を、またえいや、と開く
(3) 調べたい単語が見つかるまで、(2) を繰り返して、範囲を小さくして行く。
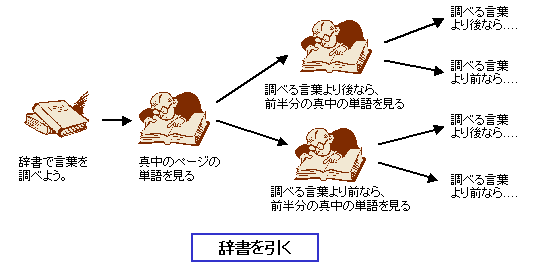
実際は、辞書には「あかさたな列」の見出しがついているので、最初の1文字で大体のあたりをつけて、その周辺を探すという方法をとっていると人が多いと思いますが、あたりをつけ終わった後、いよいよ探す範囲が狭くなると、こんな方法を使っていると思います。こういう方法を使えば、全部の単語を調べる必要なんてないんですよね。(この方法は、学術的には「2分探索」と呼ばれています)
コンピューターでも、プログラムの設計を変えれば、こういう方法で単語を検索できます。一回、真中を開くと、調べる範囲が半分に減るので、真中を開く回数は、単語数を n とすると、log2 n 回になります( log を知らない人は、気にしないで先を読んでください)。広辞苑の23万単語の場合は、18回、真中をえいや、と開けば、調べたい単語が出てきます。このスピードの違いはすごいですね。かたや 23万回の計算、それに比べて、かたや 18 回。1万倍くらい違います。
そうすると、今一週間かかる計算が、ひょっとしたら、アルゴリズムを工夫しただけで、1分で解けるようになるかもしれません。最近のスーパーコンピューターを1億円くらいで買っても、パソコンの1万倍くらいしか速くなりませんから、なにかしらの計算の工夫でスーパーコンピューターを買うのと同じ効果が得られるかもしれないのです。全ての計算が速くなるわけではないですが、工夫すれば、早くなる可能性はあるわけです。
このように、いろいろな計算が(プログラムの書き方を変えただけで)どこまで高速に計算できるのか、また、高速に計算できる場合は、どんな性質を満たすのか、同じような計算でも、計算速度が大幅に異なってしまうのはなぜなのか、理論的に算定した計算時間と、実際に実験してみた計算時間がどの程度違うのか、そんなことを研究するのが、アルゴリズムの研究なのです。
![]()