![]()
組合せ最適化
![]()
物事を決めたり、計画を立てたりするときに、いくつかの選択肢なり候補の中から、いくつかの項目を選ぶ、というタイプの物があります。例えば、いくつか投資先があるときに、これとこれとこれに投資しよう、とかいうものです。す。この「選ぶ」ということを行うときには、きっと、暗黙かもしれませんが、いくつかの条件を考えているはずです。上記の投資先の例でしたら、「あれとこれを同時に選ぶとリスクが大きいからやめよう」というようにです。物事を決めるときには、このような条件を全て、あるいはなるべく満たすようなものの中で、一番良い組合せを選ぼうとしているのです。
このように、与えられた条件を満たすように項目を選び、ある基準で最も良い(最適なもの、と言います)を選ぼう、というものが組合せ最適化問題です。組合せとしては、例えば、ある機械を使う/使わない、この場所を選ぶ/選ばない、ものを購入する/しないなどの項目がたくさんあり、この組合せを考える、といった感じです。条件のほうは、例えば、決められた予算があって、買うものの値段の合計が、予算の金額を超えてはいけない、作業をするときに、同じ機械で同時に2つの仕事はできない、この場所を選ぶとあの機械は使えない、等です。こういった条件を満たすように、コストなり、かかる時間(目的関数といいます、どんなものを最小にするかは自分で決めます)が最小になるような組合せを選びましょう、というものが組合せ最適化問題で、現実での活動や計画などを組合せ最適化問題にモデル化して、それを解くのが組合せ最適化です。
組合せ最適化問題は、企業活動に現れる様々な場所に現れます。具体的な例として、離散生産・輸送計画、スケジューリング、配送計画などがあげられます。それらについて、簡単な解説をしましょう。詳しい解説については、それぞれの解説ページを用意しましたので、そちらを読んでください。
離散生産・輸送計画は、例えれば、工場と小売を持つメーカーが、今期の各工場での生産の計画を立てるときに用いるものです。各工場での生産能力の上限と下限、各小売店での売上、各工場・小売店間の輸送コストがわかっているときに、どこの工場でどれくらい品物を作り、どこの小売店にどれだけ運べばコストがもっとも小さくなるか、という工場の生産量と輸送ルートを最適化する問題です。
スケジューリング問題とは、例えば、ある工場で、いくつか受注した仕事があり、それらの仕事をどの機械を使って誰がどの順番で行うかを、納期遅れが出ないように、残業が少なくなるように、などの目的関数を最小化するように決める問題、つまりは、最適な工程表を作る問題です。その他、時間割や人の割り当てを決めたり、航空会社でのクルーの勤務表を作る問題も、スケジューリング問題に含まれます。
配送計画は、物流会社などで、荷物の集積所から小売店に物品を配送、または回収するする際に、何台のトラックでどのようなルートを通って回収を行えば、トラックの台数・ドライバーの勤務時間・小売店への到着時刻などを最適化できるか、という問題を解くものです。付随する条件がいろいろと研究されていて、トラックの最大積載量、トラックの走る距離、小売店を訪れるトラックの種類、などさまざまな条件を付随させています。
生産・輸送計画では、工場での生産量と輸送コストが、品物の数に比例しているようであれば、これは線形計画法で解けるので、商用のソフトを使えば簡単に最適な解が求まります。しかし、現実には、生産量はロット単位で指定されていたり、運賃もロット単位で効いてくることが多いので、素直に線形計画法にはならないことが多いものです。その他にも、例えば、ある工場から輸送する小売店の数は5軒までにしてほしいとかそういった制約条件を考えると、これも線形計画の枠組みでは表せません。これらの条件を加味した問題を何とかして解こう、となると組合せ最適化問題として捉えなければいけません。
このように、企業活動や社会環境のいくつもの問題が組合せ最適化問題として捉えられ、研究されてきています。企業活動の、どんな問題でも組合せ最適化として捕らえられるわけではありませんが、目的なり制約なりがある程度数値化、あるいは組合せ的に表現できるのであれば、組合せ最適化問題として考え、最適化してみる価値は十分にあります。
組合せ最適化は、線形計画のように、高速に最適解が求まることは、まずありません。しかし、近年、近似解法という方法が研究されてきていて、これを使うと、最適解である保証はないが、かなり良いだろうと思われる解、というものは短時間で求めることができます。企業活動の問題に現れるような、大規模な組合せ最適化問題の場合、人間が解くと、1日2日かけて一生懸命解いても、あまり良い解が得られない、ということが多いものです。近似解法を用いれば、1時間程度で、だいたい、人間が解くよりも良い解を得ることができます。その結果、例えばコストが1割削減できるプランが見つかった、となれば、年間コストが1億なら、1000万円のコスト削減を行えるわけです。
組合せ最適化は、線形計画や2次計画と異なり、精度の良い商用のソフトはあまり出ていません。組合せ最適化問題は、それぞれ独特の癖があって、なかなか、どの問題も精度良く高速に解けるソフト、というものは作れないのです。組合せ最適化は、非線形計画の1種ですので、非線形計画を解くソフトを使う、という手もありますが、ちょっと問題が大きくなると、とたんに良い解が出なくなり、企業活動で出てくるような、大きな問題は解けなくなります。組合せ最適化には、それぞれの問題にあった近似解法を使うことが重要なのです。さらに、近似解法自体も、アルゴリズムを工夫して、高速化しなければ、実用上はなかなか使えるものにはなりません。
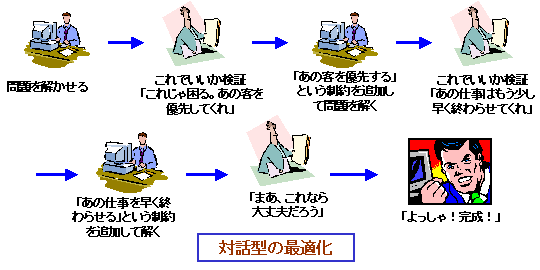
現実の問題を組合せ最適化問題として解く場合、問題を解きたい人が思っているような解をコンピューターがそのまま出してくれることは、普通はありません。条件や目的を数値化しているので、どうしても、人間が良いと思うこととコンピューターが良いと思うことにギャップができてしまい、人間が見るとよろしくないような解をコンピューターが出してしまうからです。そこで、通常は、コンピューターの出した答えを人間がチェックして、「この部分は良いがこの部分はよろしくない」という点を探し出し、そういった解を出さないよう、条件を新たに付加してコンピューターに問題を解かせなおす、といった方法が行われます。こうして、コンピューターと対話して、人間の、あいまいな条件をコンピューターに理解させていくのです。そのためには、一回の問題を解く時間が、1分程度になる必要があります。一回解くのに10分も20分もかかるようでは、対話している人間がいらいらしてしまいます。
計算の高速化のためには、アルゴリズムの改良やデータ構造の工夫が不可欠です。このような、対話型の近似解法に対しても、アルゴリズムの改良が、計算時間を10倍にも100倍にもする可能性があります。実際、データ構造を用いて、問題の大きさ(変数の数)が10000もの大規模な問題が、2-3分で解けるようにもなってきています。今後研究を進めれば、各種の組合せ最適化問題がそれこそ瞬く間に解けるようなソフトが開発されていくでしょう。
![]()