![]()
組合せ最適化とは何でしょうか
![]()
与えられた条件を満たすような組合せなり順番なりを選ぶとき、選べる組合せの中から一番良いものを探し出しなさい、という問題を、組合せ最適化問題といいます。数式で表現するならば、ある集合 E の部分集合 F で、与えられた条件を満たし、かつ関数値 f(E) を最大、あるいは最小にするものを求めなさい、という問題になります。組合せ最適化とは、現実での活動や計画などを組合せ最適化問題にモデル化して、それを解く、つまり、一番良い選択肢を選ぶものです。
世の中の社会現象や活動を組合せ最適化問題として捉えるにはどうすればいいか、はたまた組合せ最適化問題をなるべく短時間で解くためにはどうすればいいか、あるいは各種の組合せ問題がどのような性質を持っているか、高速解法構築のためには、どのような性質が役に立つか、といったことを研究するのが、組合せ最適化の研究です。
集合の中から組合せを選ぶっていうのはいったい何だ、と思う方もいるだろうと思いますので、まずは簡単な例を紹介しましょう。
Sさんが、家の不要品を集めてフリーマーケットに持って行き、売ろうと考えています。集まった不要品は以下の通りです。値段もつけてみました。全部を持って行ければいいのですが、会場までは自転車で行かなければいけないので、そんなにたくさんの荷物はもてません。7kgが限界だと S さんは考えています。それと、傘とほうきとラケットは長くて荷物に入れづらいので、どれか1つしか持って行かないことにしました。なるべくたくさんお金が入ったほうがいいので、売値の合計がもっとも大きくなるよう、荷造りをしたいと思っています。さて、どういうふうに荷造りをすればよいでしょうか?

これは、「持っていく不要品の組合せで、もっとも良いものを選ぶ」ので、組合せ最適化問題です。数学的に考えれば、
荷造り(解) S は、不要品の集合 E の部分集合
評価値(目的関数)は、S に含まれる不要品の売値の和
制約は、
S に含まれる不要品の重さの和が 6kg 以下
S は、ほうき・ラケット・傘のうち、高々1つしか含まない
となります。制約を守っていて、評価値(目的関数と言います)が一番良い物を見つけなさい、という問題なわけです。
さて、では実際に一番良い荷物の組合せを見つけだすにはどうしたらいいでしょうか? いちばん簡単に思いつき、かつ確実な方法は、「すべての組合せを1つ1つチェックして、しらみつぶしに探す」だと思います。この例だと、物が8個ありますから、2の8乗、つまり256通りの組合せを全てチェックすれば、必ず一番良いものが見つかります。しかし、この方法だと、あまりにも工夫がないので、もう少し工夫を入れた、分枝限定法という方法を見てみましょう。
不要品の中でビデオに注目して、荷物の組合せを、ビデオを入れるものと、入れないものに分けて考えます(この「分けて考える」ことを分枝と言います)。まず、ビデオを入れた組合せの中で、もっとも売値合計が大きいものを見つけます。次に、ビデオを入れない組合せの中でもっとも売値合計が大きいものを見つけます。で、両者を比べて、売値合計が大きいものを見つければいいわけです。
さて、ビデオを入れた組合せの中で、もっとも売値合計が大きいものを見つけるにはどうすればいいでしょうか?再帰的に、次はラケットに注目して、ラケット(とビデオ)を入れた組合せと、ラケットを入れない(ビデオは入れる)組合せに分けて考えればいいわけです。このように繰り返し分解していけば、一番良い組合せを求めることができます。
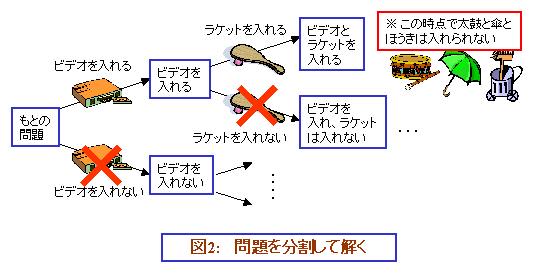
この方法、このままだと、しらみつぶしに調べているのと同じになります。が、例えば、今説明した、ラケット(とビデオ)を入れた組合せを調べるとき、すでにラケットとビデオを合わせて 5kg あるので、太鼓は入れられない、という新たな条件が出てきます。もう、太鼓は考えなくていいわけですので、手間がちょっと減りますね。それと、この時点で荷物にラケットが入っているので、ほうきと傘も入れられない、という条件も付きます。ほうきと傘の分の手間も省けるわけです。このように、「必ず入る不要品」「必ず入らない不要品」を見つけていけば、調べる組合せは減ります。それで、計算の高速化ができるわけです。
こういう、なるべく無駄なチェックをしないで、一番良い組合せを見つけるにはどうすればいいか、速く解ける問題はどんな性質を持っていて、同じ性質を持っている問題はなんなのか、といった研究をするのが、組合せ最適化の研究です。世の中の問題をどうやって組合せ最適化問題に変換するか、企業などで使われる大きな問題を高速に解くにはどうしたらいいか、などの研究も行っています。
例えば、上記のフリーマーケットの問題も、拡張して考えると、倉庫の中に品物があって、そのうちのどれを小売店に出せばいいか、という、プラニングの問題も出てきます。なんとなく、企業活動で出てきそうな問題です。さらに、小売店がいくつかあって、それぞれにどの品物を送るか、とか、いくつか余計に生産できれば、品物を製作料を引いた、売値の総和をもっとも大きくしたい、とか、変化させていけば、いろいろな問題が考えられます。こういった問題の中から、企業活動や、環境調査、研究上などで比較的良く現れるタイプの問題を探し出し、特徴付けをして、それらの問題について、研究を進めていくのです。例えば、このサイトで解説している配送計画、スケジューリング問題、生産計画などがそうです。
これら、限定された問題でも、最適な解を求めるにはまだまだ時間がかかります。ですので、これらの問題に関しては、問題の構造の研究や、近似解法の研究が盛んに行われています。組合せ最適化問題は、制約条件を緩めてあげると、線形計画問題に変換できます。線形計画は短時間で解けるので、この、緩めてできた線形計画(緩和問題といいます)と、もとの組合せ最適化問題の関係を調べたり、緩和問題の解がもとの組合せ最適化問題の解と近くなるためには、どのように条件を緩めればいいか、といった方向からも研究が行われています。近似解法も、様々な問題に、様々な方法が提案されていて、実用上使えるものがずいぶんと出てきました。
これらの組合せ最適化解法や近似解法に対しても、アルゴリズムの高速化は有効です。同じ原理に基づいて作られたプログラムでも、アルゴリズムによって速度が向上するからです。問題の構造から得られた知識では、速度の面で目標が達成できなくても、アルゴリズムの改良が、その後押しをできるからです。最適化解法、近似解法ともに莫大な数の方法が発見されてきているので、アルゴリズム的な研究は、これからどんどん、やることがあるわけです。
![]()