![]()
最適化
![]()
最適化とは、物事の計画を建てたり、作業をしたりするときに、どのようにすると一番楽かとか、もうかるか、を短時間で調べる問題のことを言います。大きくて複雑で、人間が解くのは大変な問題を、コンピューターを使って解けるようにしよう、というのが目標の1つなので、数理的に、すなわち、あいまいではなく、はっきりと表せるものを扱います。例えば、物をしまう(倉庫に商品をしまう)ときに、なるべく多く詰め込むにはどうしたらいいか、作業をするときに、どういう順番で行うと効率がいいか、などです。ナビゲーションシステムのように、現在位置から目的地まで、どのルートを通ると一番速いか、という問題も、最適化問題に入ります。
ちょっと、簡単な例を見てみましょう。あるところに、家具工場がありました。この工場で、今、今月は何を何個作るか、作業計画を立てています。何を作るにはどれくらい材料が必要で、どのくらい時間がかかるか、それと、作るとどれくらいもうかるか、を図にまとめてみました。この工場、仕入れの関係から、どの材料にも、使える量に限りがあります。また、作業時間も、労働環境の関係から、制限があります。それも図に書きました。
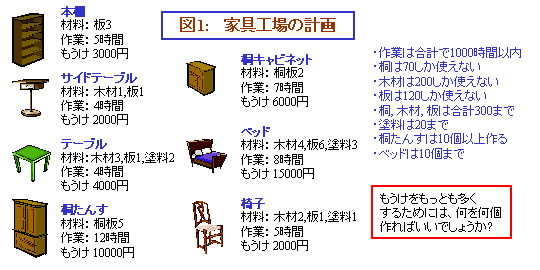
さて、この工場で、今月のもうけを最大にするには、どの家具を何個作ればいいでしょうか?
この問題では、「それぞれの家具を何個作るか」と、個数というハッキリと表せるものを最適化しようとしています。個数なら数字で表せますから、数学的に表現できますね。制限のほうも、数学的に、簡単に表現できます。使う材料数はは何個以下とか、そういった条件ですから、不等式でかけます。つまり、
(桐たんすを作る個数) × 5 + (桐キャビネットを作る個数) × 3 = 使う桐板の枚数
(桐板の枚数) ≦ 70
というように、数式で書けるわけです。もしこれが、「お客が気に入るようにする」とかいうあいまいな条件があると、お客が気に入るようにするにはどうすればいいんだ、という話になって、人間系でないとうまく解けません。逆に、こういう、数式なり、あるいは論理式、つまり「あれとこれが成り立つ」「あれかこれが成り立つ」というような条件式だけで、制約になる条件が構成されているならば、コンピューターで扱えるわけです。
最適化、という方法は、世の中のいろいろな問題に適用できますが、中でも、企業活動の中に現れる問題には、最適化が適用できるものが多いのです。最適化で扱えるものは、上記の例のような「個数」という物ばかりでなく、物事や作業を行う「順番」、あるいは客や配送先を回る「順番」、買う/買わない、使う/使わない、休ませる/運転する、などの「選択」、あの機械でこの作業、あのトラックにこの運転手、などの「対応付け」、誰と誰と誰をプロジェクトに派遣するか、どの工場とどの工場とどの工場を操業するか、などの「組合せ」、ここからあそこまでどこの道を通るか、などの「ルート選択」など、多岐にわたります。また、最適化したいもの、つまりコストとか、時間とか、そういったものも、企業活動に現れる問題では、比較的分かりやすいものが多く、数学的に表現しやすいのです。
しかしながら、現実の問題を直接最適化問題に直して解く、ということは、通常、あまりできません。なぜなら、どの問題にも、多少はあいまいな部分があるからです。そういったあいまいな部分を上手に取り込んで最適化問題を作らないと、なかなか実際には役に立たちません。
例えば、車のナビゲーションシステム。あれは、最短ルートを見つけているわけですが、その際に、あいまいな部分、複雑な条件で、答えに対する影響が微小なもの、これらをずいぶんカットしています。例えば、車の速さ。都市部の太い道では平均時速30km程度、細い道では20kmといったように設定されているはずです。本当は、その道の信号の数、信号の変わるタイミング、さらには運転手の技量まで考えないと、正確な速度は出ないのですが、そんなに細かく考えても、なんかのひょうしに車がスピードを落としたり、あるいは脇に駐車している車がいたりするだけで速度は変わってきますので、実際には意味のあるものが出てこないのです。さらに、ルートを選ぶときは、走りやすいルート、というものを選ぶほうがいいのですが、どのようなルートが走りやすいかは人によって違いますので、うまく選べないのです。ナビゲーションシステムでは、こういった困難な面には目をつむり、目的を「きわめて短時間で、それなりに早く行けるルートを見つける」ということに絞っている点が、成功しているポイントでしょう。
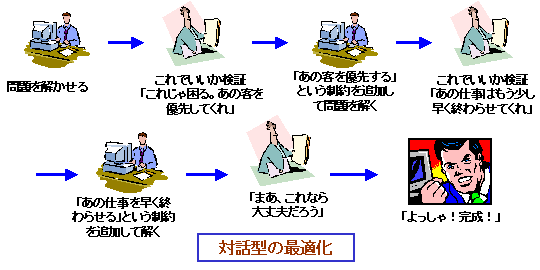
企業などの最適化では、こういった、あいまいな、あるいは表現しづらい条件が良く現れます。そういった部分については、人間が解くほうが良いのです。その反面、大きな問題、あるいは短時間で解く必要がある問題は、コンピューターで解くほうが良いのです。この両方、表現しづらい条件もあるし、大型だ、という問題を解くにはどうすればよいでしょうか。1つの良い方法は、簡単な条件だけを入れた問題をコンピューターに解かせて、出てきた答えを人間がチェックし、「この部分は良いがこの部分はよろしくない」という点を探し出し、そういった解を出さないよう、条件を新たに付加してコンピューターに問題を解かせなおす、といったものです。こうして、コンピューターと対話して、人間の、あいまいな条件をコンピューターに理解させていくのです。
最適化問題にも、解きやすい問題と、解きにくい問題があります。解きやすい問題の代表格は、線形計画というものです。線形計画問題は、最適化する目的、つまり、もうけとか、守らなければいけない条件の式に、2乗とか3乗とかがついていない、上記の式のようになっているものをいいます。本当は、もう少し条件がもうちょっとつきます。上記の家具工場の例は、線形計画問題になっています。この他、凸2次計画という問題も研究されていて、比較的短時間で解けるようになりました。

このように、最適化問題の中でも、いくつかのものは、商用のソフトを使って短時間で解けまから、家具工場の計画も、品数が莫大に増えて、条件もたくさんになっても、だいたい簡単に一番良い計画が見つかるわけです。しかし、世の中、そう簡単なものばかりではありません。一般に、企業活動なで、実際に解きたいな、と思うような問題は、どちらかというと、線形計画や凸2次計画にはならないものの方が多いのです。
このように、簡単には解けない最適化問題として、整数計画や組合せ最適化というものがあります。物を買う個数、作る個数などが、最適化したい変数に入っている場合、「0.7個買う」とか「0.15台作る」とかいったものは実現できないので、「これらの個数は整数になること」という条件をつけるものです。良くある条件ですので、整数計画が速く解けるとうれしいのですが、残念ながら最適な答えを見つけるには、変数が100程度でも、パソコン程度では到底解けなくなります。スーパーコンピューターでも、かなり苦しいでしょう。たとえ今のコンピューターの速度が1万倍になっても、解ける問題の大きさは、20ぐらいしか増えません。コンピューターの高速化がいくら進んでも、こういう問題を解く、という観点からは、絶望的なわけです。
こういった難しい最適化問題をいかに速く解くか、という研究も行われています。まだまだ、大きな問題が解けるレベルにはなっていないのですが、それでも、何も考えずにプログラムを組むよりは、1万倍も、1億倍も高速に問題を解けるようになりました。
難しい最適化問題に対しては、近似解法という方法も研究されています。これは、「たとえ最適な答えでなくてもいいから、短時間で、最適になるべく近い答えを見つけよう」という方針で設計されたものです。短時間で、ある程度良い答えが見つかるのが特徴なのですが、どれくらい最適なのか、つまり精度に関してはなんの保証も得られないことが多い、というのが難点です。この問題の最適な答えを知りたい、という目的には使えませんが、例えば、今のプランよりも良いプランがあったら、それに乗り換えたい、という目的の時には、問題なく使えます。こういった近似解法も、精度をなるべく良くして、大きな問題を解こうとなると、時間がかかります。上記の「対話型の最適化」を行うためにも、高速なソフトはかかせません。遅いソフトを使うと、対話している人がいらいらしてしまいますし、時間も大幅にかかるからです。
こういったソフトを高速化するには、アルゴリズムの研究がかかせません。いくら良い発想に基づいた方法を使っても、高速化の技術がなければ、大きな問題を短時間で解くことはできないからです。現在、企業活動の一部で最適化が使われています。しかし、そこで使われているソフトは精度の良くないもの、速度の遅いものなどが多くあります。ゆえに、最適化は時間がかかり、使い物にならない、という印象を持つところもあるようです。しかし、良く現状と目的を分析して最適化モデルを作り、ちゃんとした技術を用いたソフトを使えば、短時間で良い解が得られる、そんなシステムが作れるのです。
![]()