Graph Golf: The Order/degree Problem Competition

Problem statement

Update 2021-04-20

Definition

The order/degree problem with parameters n and d: Find a graph with minimum diameter over all undirected graphs with the number of vertices = n and degree ≤ d. If two or more graphs take the minimum diameter, a graph with minimum average shortest path length (ASPL) over all the graphs with the minimum diameter must be found.

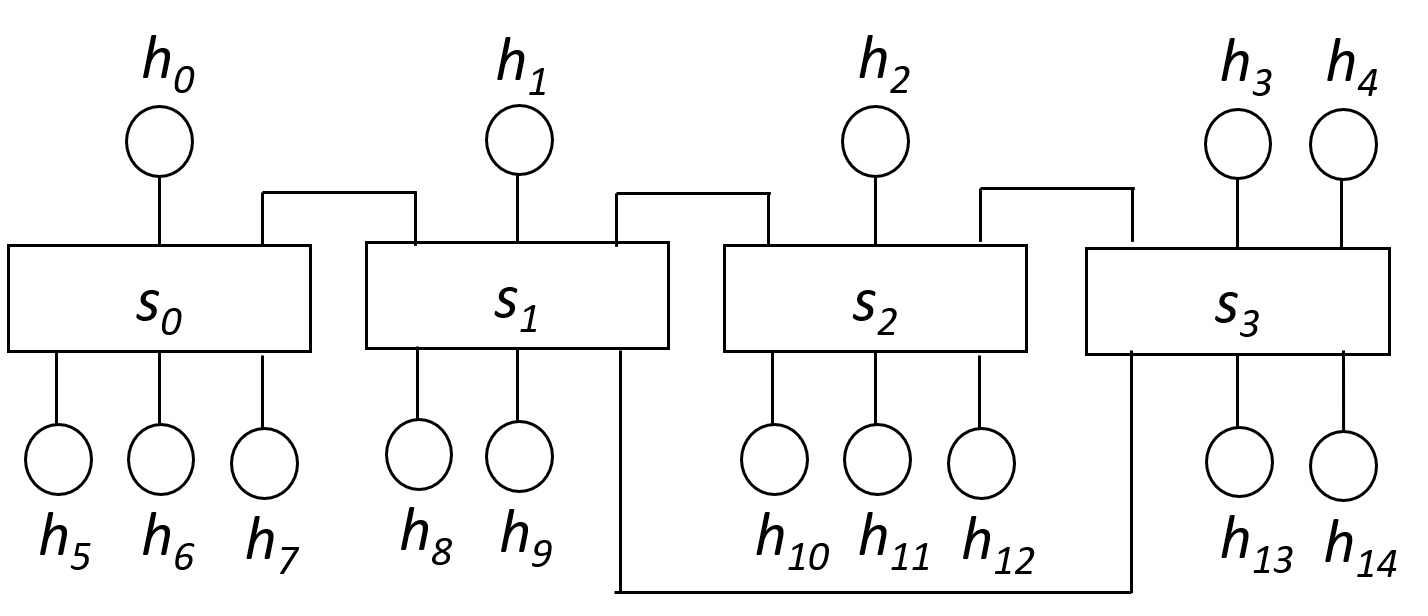
The order/radix problem on a host-switch graph with parameters n and r: A host-switch graph represents a network topology of computer systems with 1-port host computers and r-port switches. Formally, a host-switch graph is a 3-tuple G=(H, S, E) with integer parameters n ≥ 3, m ≥ 1, and r ≥ 3 where

H = {h₀ , h₁ , ..., h_n-1} is a set of n elements called host vertices (or simply hosts),
S = {s₀ , s₁ , ..., s_m-1} is a set of m elements called switch vertices (or simply switches), and
E ⊂{{s_i , s_j} | s_i , s_j ∈ S} υ {{h_i , s_j} | (h_i ∈ H) ∧ (s_j ∈ S)} is a set of elements called edges.

The number n of hosts is called the order of G. The number r of ports per switch is called the radix of G. Each host must be connected with exactly one edge while each switch is connected with at most r edges. The objective of the order/radix problem is to find a host-switch graph with minimum host-to-host diameter (h-diameter) over all undirected host-switch graphs with order = n and radix ≤ r. If two or more host-switch graphs take the minimum h-diameter, a host-switch graph with minimum host-to-host ASPL (h-ASPL) over all the graphs with the minimum h-diameter must be found.

Example

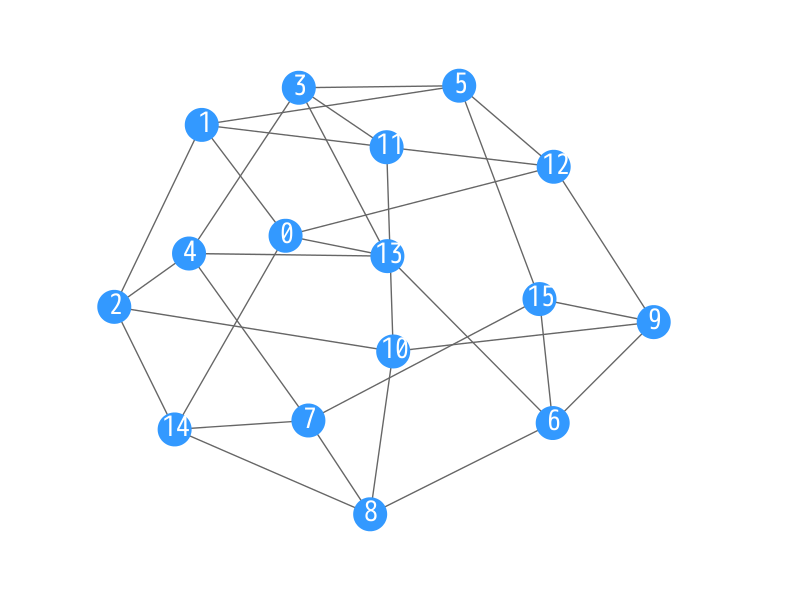
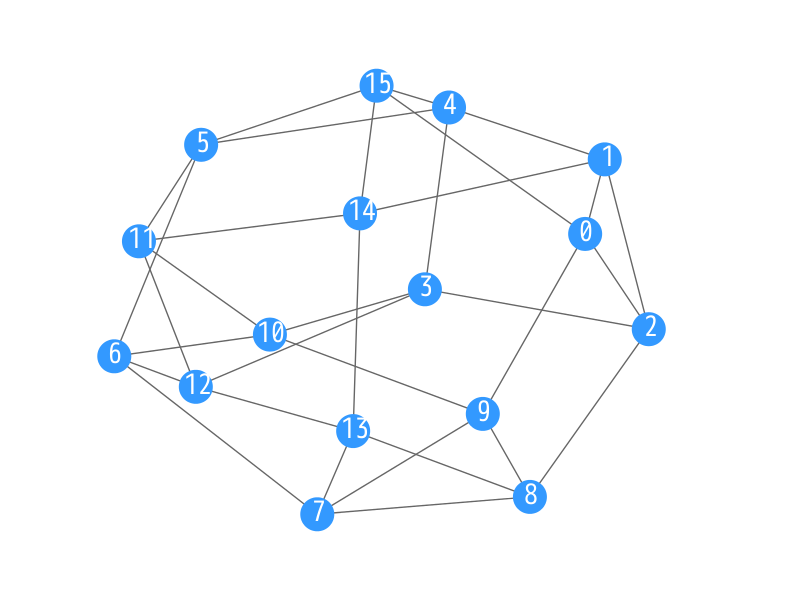
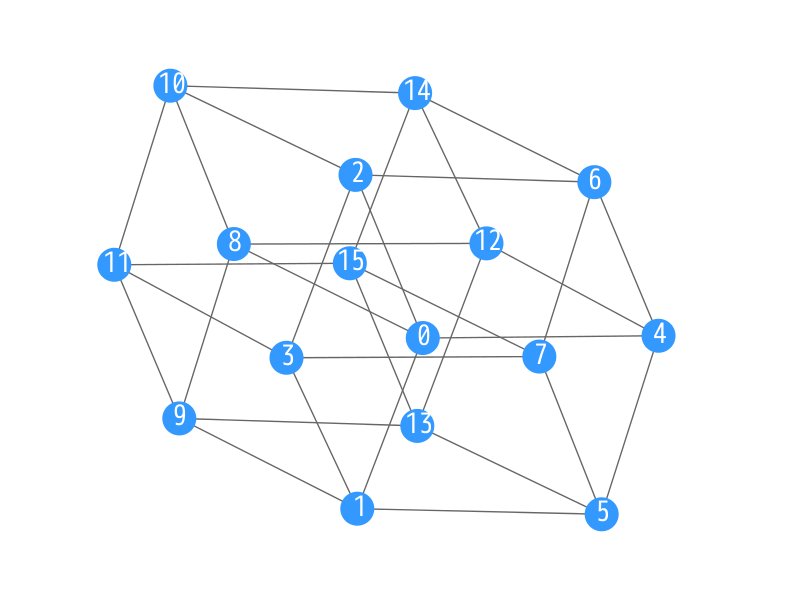
Let us show examples for the order/degree problem with parameters n = 16 and d = 4. The figure illustrates three examples of 4-regular graphs with 16 nodes. The diameter of the first and the second graphs is 3, while that of the third one is 4. Thus, we should select the first or the second one. Next, we compare the average shortest path length (ASPL) of those two graphs. Since the ASPL of the first one is smaller, this is the best solution of the problem among the three.


Graph
Diameter	3	3	4
ASPL	1.942	1.983	2.133

We illustrate an example of a host-switch graph with 4 switches with order n = 15 and radix r = 6. The h-diameter and h-ASPL is 4 and 3.104762, respectively.

Why order/degree problem? Why order/radix problem?

Graph design has a rich variety of application fields of computer systems. In particular, it is just meeting a network design of future supercomputers and future high-end datacenters in terms of hop counts [SOCC11] [ISCA12] [SC14], [TPDS19], since their networks are topologically modeled as undirected regular graphs or host-switch graphs. Low latency is preconditioned on small hop counts, but existing network topologies have hop counts much larger than theoretical lower bounds. Therefore, computer network designers desire to find a graph that has a small number of hops between any pair of vertices.

Why not degree/diameter problem?

The degree/diameter problem (DDP) has been studied for decades and consists in generating the largest possible graph given degree and diameter constraints, striving to approach theoretical upper bounds [DDP-wiki]. However, DDP solutions may not be directly usable for network topologies in supercomputer and high-end datacenter systems because they are for particular number of compute nodes, whereas the number of nodes in a real system is determined based on practical considerations, e.g., budget.

Lower bound of diameter & ASPL

For a general graph with order n and degree d, the lower bound K_n,d on diameter k is computed as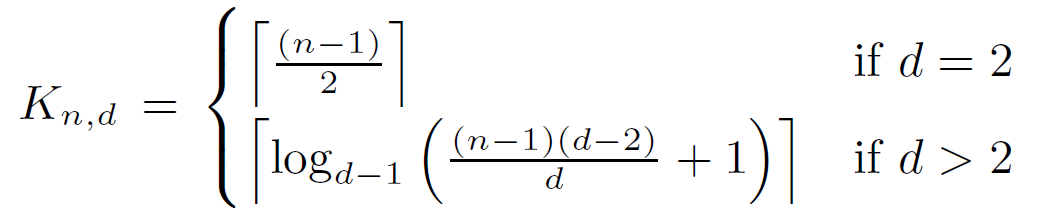

Similarly, the lower bound L_n,d on ASPL l is computed as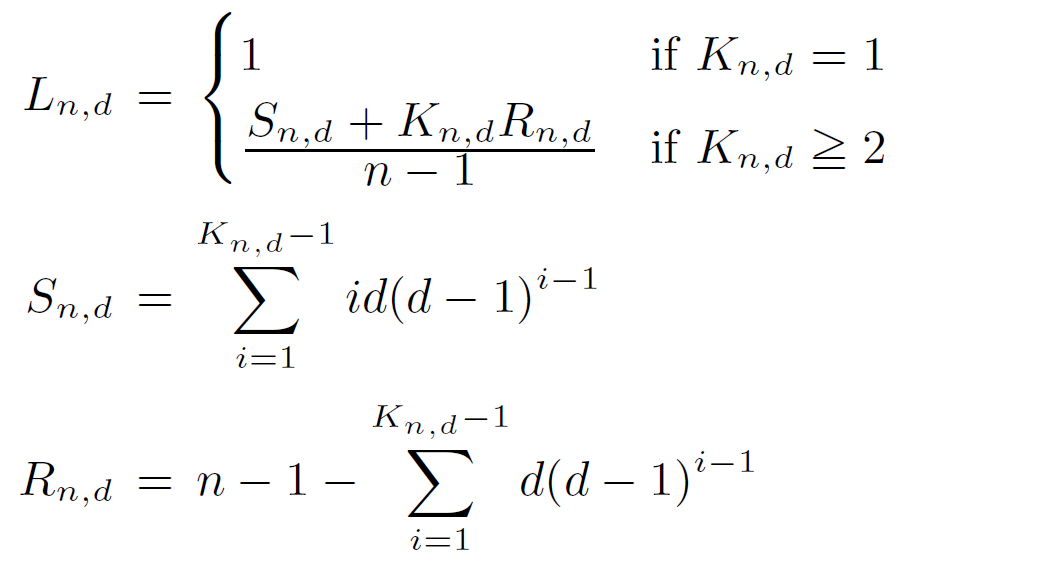

For a host-switch graph with order n and radix r, lower bounds on h-diameter and h-ASPL can be computed by the algorithm shown in [TPDS19]. We employ these lower bounds for the host-switch graph category of the competition.

Programs for calculating those lower bounds are provided below.

Programs

A Python script that generates a regular random graph and calculates its diameter and ASPL is provided here. This may be a good starting point if you are new to creating graphs.

create-random.py (requires NetworkX)

For a faster calculation of ASPL, a C++ program was developed by Ryuhei Mori, and an MPI-based parallel program was developed by Masahiro Nakao.

A C++ program that generates a random host-switch graph and the lower bound. Another C++ program that calculates h-diameter and h-ASPL of a given host-switch graph are developed by Ryota Yasudo.