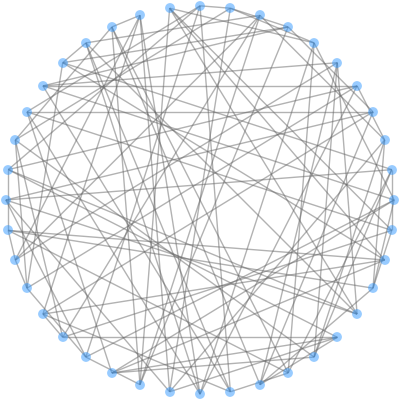
Find a graph that has smallest diameter & average shortest path length given an order and a degree.
News
- 2021-10-11: 7 solutions accepted! Now we concluded the 2021 competition! Check out the final rankings
- 2021-10-04: 1 solution accepted!
- 2021-09-27: 1 solution accepted!
- 2021-09-06: 4 solutions accepted!
- 2021-08-30: 1 solution accepted!
- 2021-08-23: 1 solution accepted!
- 2021-08-09: 1 solution accepted!
- 2021-08-02: 9 solutions accepted!
- 2021-07-26: We modified and used the progoram host-switch-aspl to calculate h-diameter and h-ASPL of a given host-switch graph for ease of identifying errors.
- 2021-07-26: 66 solutions accepted! Now we enter the open submissions period!
- 2021-04-27: Announced the 2021 competition!
Archives
Update 2024-01-09
Welcome!
Notice: We do not open the Graph Golf competition in 2022.Pickup solutions
Motivation
Graph design has a rich variety of application fields of computer systems. In particular, it is just meeting a network design of future supercomputers and future high-end datacenters in terms of hop counts, since their networks are topologically modeled as undirected regular graphs. Low latency is preconditioned on small hop counts, but existing network topologies have hop counts much larger than theoretical lower bounds. Therefore, computer network designers desire to find a graph that has a small number of hops between any pair of nodes. How to minimize the diameter and the average shortest path length (ASPL) of a graph given the order (the number of nodes) and the degree (the number of edges at each node)?
Competition
Graph Golf is an international competition of the order/degree problem since 2015. It is conducted with the goal of making a catalog of smallest-diameter graphs for every order/degree pair. Anyone in the world can take part in the competition by submitting a graph. Outstanding authors are awarded in CANDAR'21, an international conference held in Matsue, Japan, in November 2021.
Let me challenge!
The 2021 contest has finished.
Schedule
- 2021-04-27: Closed submission period starts
- 2021-07-26: Open submission period starts
- 2021-10-11: Submission period ends (deadline 2021-10-11 23:59:59 UTC)
- 2021-10-18: Awards notification
- 2021-11-23(tentative): Workshop in CANDAR'21